#LeetCode: Maximal Square

Given a 2D binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

Example:

Input:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

Output: 4

Let's try to solve this by using the memorization table.

1). Create a memorization table memoTable [r][c], where r is the number of rows in input array and c is the number of columns in input array.
2). The value at any position of memoTable will depend on a couple of conditions:

Let's create a memorization table for the example:

The value at any position of memo table depends on:
1). Value at the same position of input array.
2). Value at the top position of memo table.
3). Value at the left position of memo table.
4). Value at the left top diagonal of memo table.

Algorithm:
1). Instead of creating a memo table of r*c, we will create an array of length c (where c is the length of input array).
2). a variable maxSquare will hold the maximum value present in the memo table.
3). a variable leftTopDiagonalVal will contain the value of the left top diagonal of current position from the memo table. We will pre-populate the leftTopDiagonalVal with the value at first position of input array (matrix[0][0]).
4). a variable 'temp' will hold the value at jth position of memo table, where j is the current column index.
5). Now we will start iterating. For the first row and first column, we will copy the value from the input array. If the value if 1, we will update maxSquare (it would be either the current value of maxSquare or the value at jth position of memo table, whichever is higher).
6). For other rows and column, if the value at the input array is zero, we will update value at jth position of memo table as zero. Else, we will take the minimum value at jth position, j-1 position of memo table and leftTopDiagonalVal, increment the minimum value with 1 and update the value at jth position of memo table. Then we will update maxSquare.
7). We will update leftTopDiagonalVal.
8). Output would be square of maxSquare.

GIT URL: Java Solution of Leet Code's Maximal Square problem

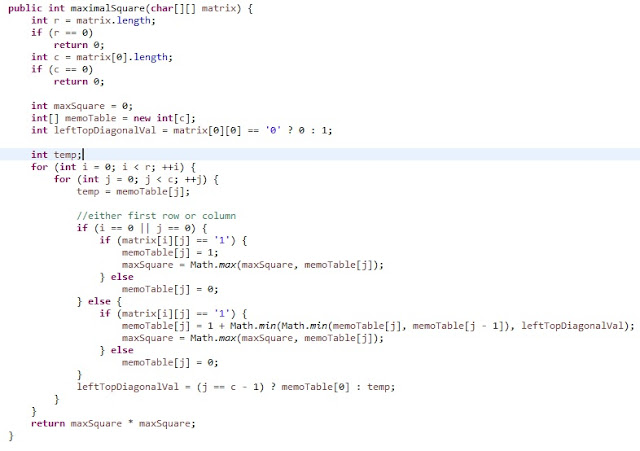
Java Solution:

ALSO CHECK: Other LeetCode Solutions in Java

-K Himaanshu Shuklaa..